NON-INTRUSIVE MODEL ORDER REDUCTION
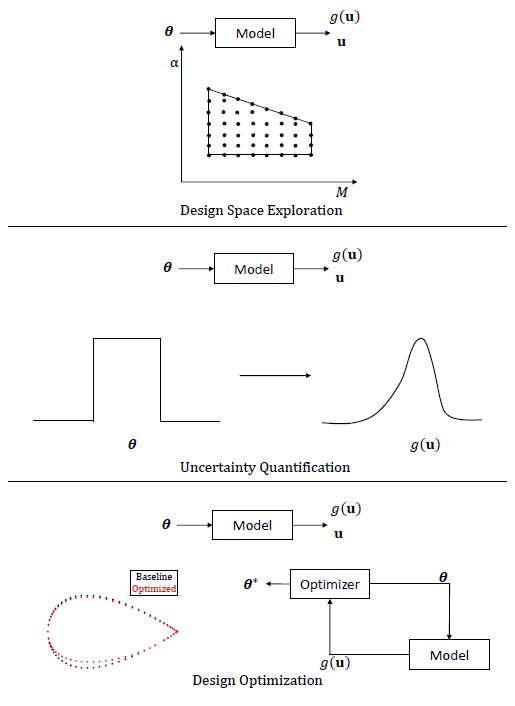
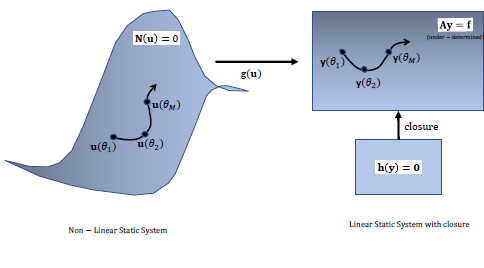
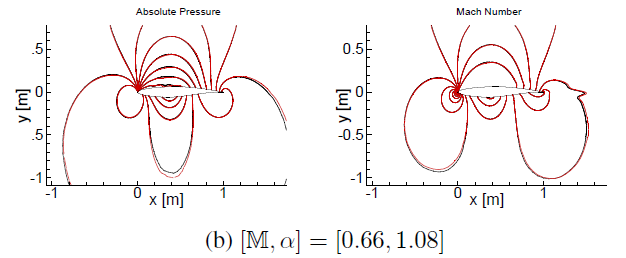
Figure: Red lines/symbols = ROM, Black lines/symbols = FOM
The projection-based reduced order modeling, typically requires access to the discrete form of governing equations of the high-fidelity model. The projection is commonly done on a subspace determined via POD. However when commercial codes are used as the high-fidelity model, such an approach is not possible in general. Usually in such circumstances, a ‘POD+Interpolation’ approach is taken where the reduced state variable is directly interpolated to adapt for change in time/parameters. This work devises a method to develop projection-based ROM with commercial codes, specifically CFD codes. The novelty of the work is that it converts the original non-linear PDE system into a linear PDE system with auxiliary non-linear algebraic equations which are then projected onto the POD subspace. By such a linearization, it is shown that the governing equations can be extracted by directly discretizing the linear terms (which is easier compared to non-linear terms) at a computational cost that scales linearly with grid size ($N$). Other methods that exist to ‘discover’ governing equations from data, are known to also involve a similar or higher cost, while being tailored towards time-dependent systems. Finally, the ROM is posed as a constrained optimization problem that can be solved cheaply. Since the work specifically addresses static parametric systems, a database of such ROMs are generated for a pre-determined set of parameter snapshots which are then interpolated by mapping them to the tangent space of the manifold they are embedded in (manifold of symmetric positive definite matrices in this case) to adapt for parametric changes. The method is tested on canonical PDEs and flow past airfoils at subsonic and transonic flow
regimes. A prediction error of < 5% was achieved in subsonic cases in terms of the state, pressure distributions, lift and drag. Under transonic conditions with moving shocks, the approach incurs higher error unless a sufficiently dense snapshot distribution is used. Model parameters are identified and experiments are conducted to determine settings that improve accuracy. The usefulness of the method is also demonstrated on application problems in the many-query context - design optimization and uncertainty quantification. Overall, the strength and weaknesses of the approach are identified, demonstrated and explained.
Publications
-
Renganathan, S. A., Maulik, R., & Rao, V. (2020). "Machine learning for nonintrusive model order reduction of the parametric inviscid transonic flow past an airfoil." Physics of Fluids, 32(4), 047110.
-
S. Ashwin Renganathan (2020). "Koopman-based approach to nonintrusive reduced order modeling: Application to aerodynamic shape optimization and uncertainty propagation." AIAA Journal, 58(5), 2221-2235.
-
S. Ashwin Renganathan, Yingjie Liu, and Dimitri N. Mavris, "Koopman-Based Approach to Nonintrusive Projection-Based Reduced-Order Modeling with Black-Box High-Fidelity Models", AIAA Journal, October 2018, Vol. 56, No. 10 : pp. 4087-4111
-
S. Ashwin Renganathan, "A methodology for non-Intrusive projection-based model reduction of expensive black-box PDE-based systems and application in the many-query context", Ph.D. Thesis, 2018, Georgia Institute of Technology. <https://smartech.gatech.edu/handle/1853/59876>
MULTIDISCIPLINARY ANALYSIS AND OPTIMIZATION
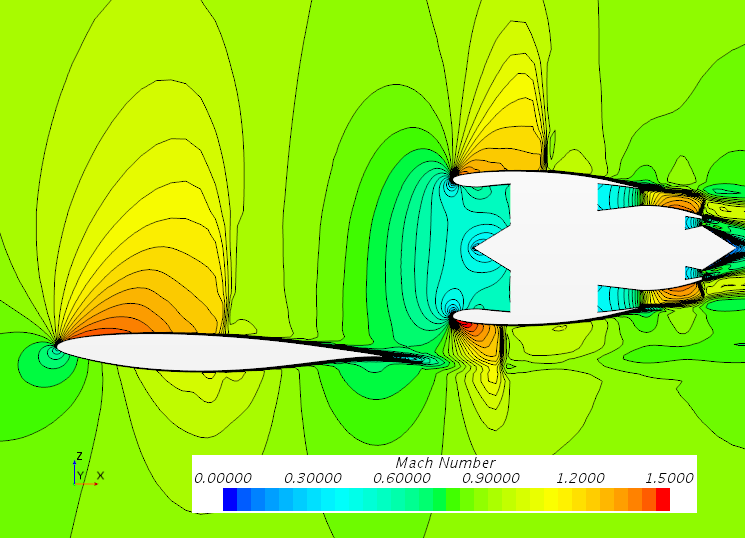

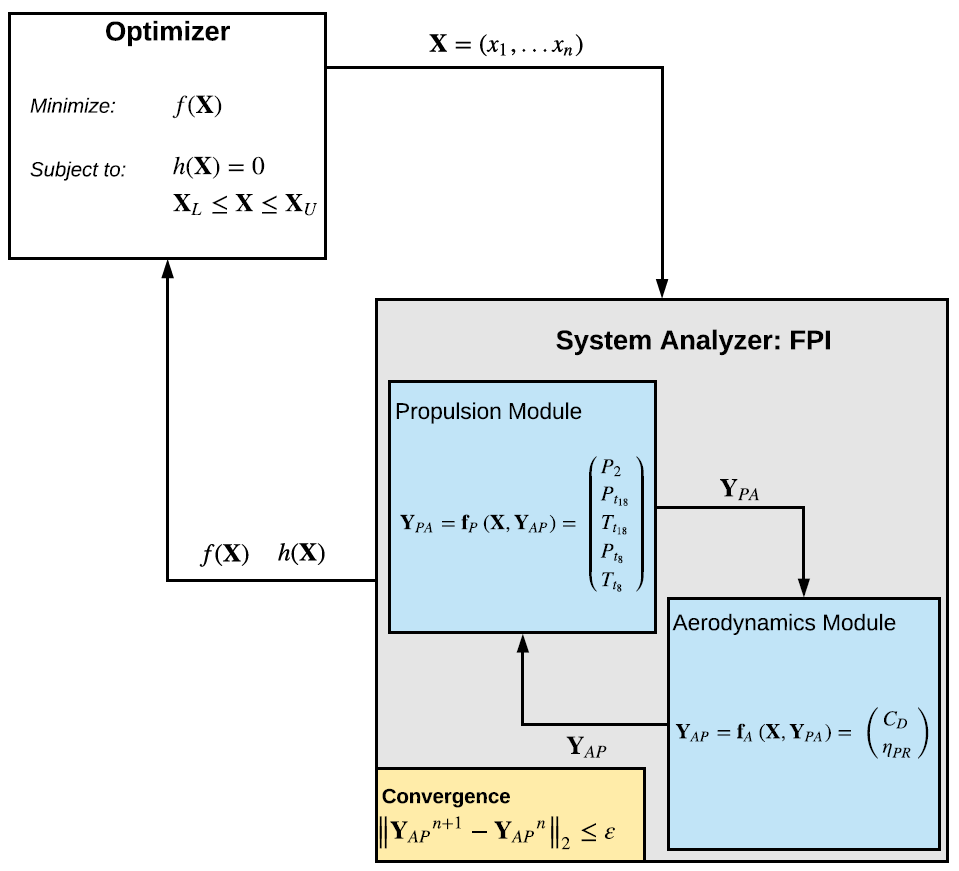

Engine bypass ratio (BPR) has grown significantly over the years, due to a desire for increased efficiency, and the large fan diameters that have resulted are forcing the engines so close to the wing that there is no room left for them to grow any larger due to ground clearance constraints. As BPR increases even further in the future, conventional Under-Wing Nacelle (UWN) installations will therefore no longer be possible without drastic modification of the wing and landing gear. Over-Wing nacelle concepts solve this problem by offering a convenient installation for high BPR turbofans and, additionally, offer the potential to mitigate community noise through engine noise shielding using the wing as a shield. However, OWN has historically warranted concern about unacceptably high drag levels at transonic speeds and the purpose of this research was to determine whether or not drag can be improved enough to take advantage of the aforementioned cross-disciplinary benefits. To do so, three studies were conducted: study 1 conducted a simple nacelle sweep in order to identify and visualize the physical mechanisms driving the configuration, study 2 then conducted a sensitivity analysis in order to understand important design variables and, finally, study 3 performed single point optimization for a trailing edge OWN concept. Overall, results suggests that OWN drag can be improved to levels commensurate with its Under-Wing Nacelle (UWN) counterpart. However, limitations of the analysis tools employed for this research (in the area of shape optimization) were insufficient to outperform the UWN baseline. Such limitations were successfully overcome by modern OWN concepts, such as the Honda Business Jet and the military Lockheed HWB for air mobility missions. Overall, it is therefore the authors' opinion that either leading-edge or trailing-edge mounted OWN configurations are concepts worth investigating further for civil transport applications.
Publications
-
Berguin, S.H., S. Ashwin Renganathan et al, "CFD Study of an Over-Wing Nacelle Configuration", Technical Report 2018, Georgia Institute of Technology. <https://smartech.gatech.edu/handle/1853/60464>
-
Jai Ahuja, S. Ashwin Renganathan, Steven Berguin, Dimitri N Mavris, "Multidisciplinary Analysis of Aerodynamics-Propulsion Coupling for the OWN Concept", 2018 Multidisciplinary Analysis and Optimization Conference, AIAA AVIATION Forum, (AIAA 2018-2927)
-
Berguin, S.H., S. Ashwin Renganathan et al, "Sensitivity Analysis of Aero-Propulsive Coupling for Over-Wing-Nacelle Concepts", 2018 AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, (AIAA 2018-1757)
STOCHASTIC OPTIMIZATION
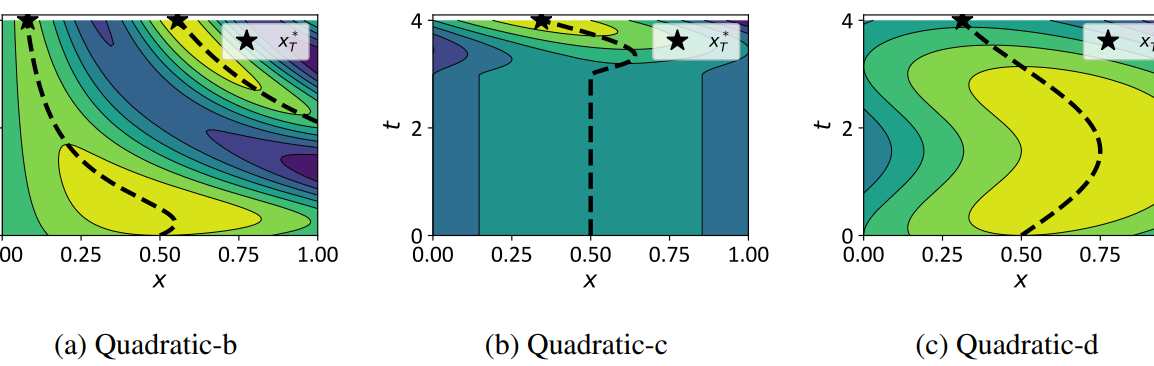
Contours that visualize the one-dimensional (X ⊂ R) time-dependent payoff function f(x, t). The dashed lines trace the location of x ∗ at every t. We are interested in the maximizer of the payoff at T, x ∗ T . Each payoff function is generated by adding a nonlinear component (dependent on x at t) to a simple one-dimensional quadratic function; see supplementary material for details.
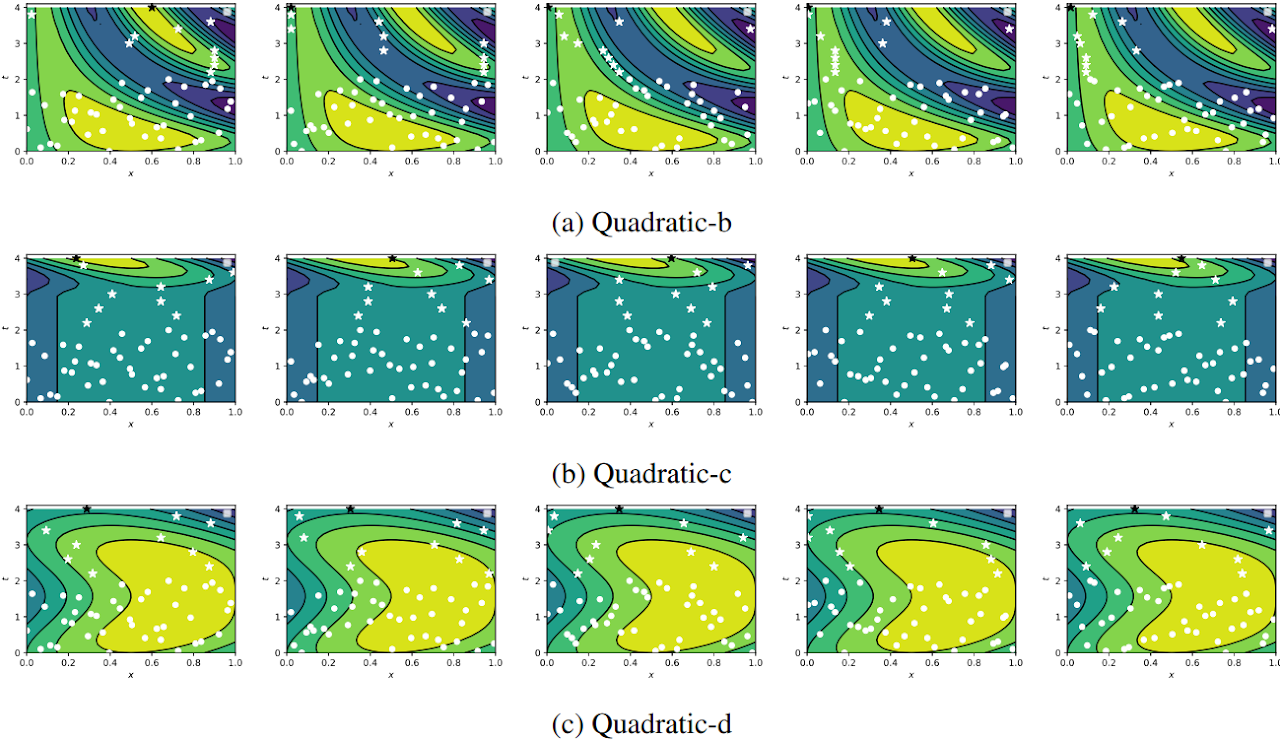
Performance of the proposed approach (r2LEY) on the 1d problems for 5 repetitions (left to right). Circles are initial samples, stars are points selected by r2LEY and the black star is the final point x ∗ T . Contours represent the true noise-free payoff function for reference.
AERODYNAMIC DATA FUSION
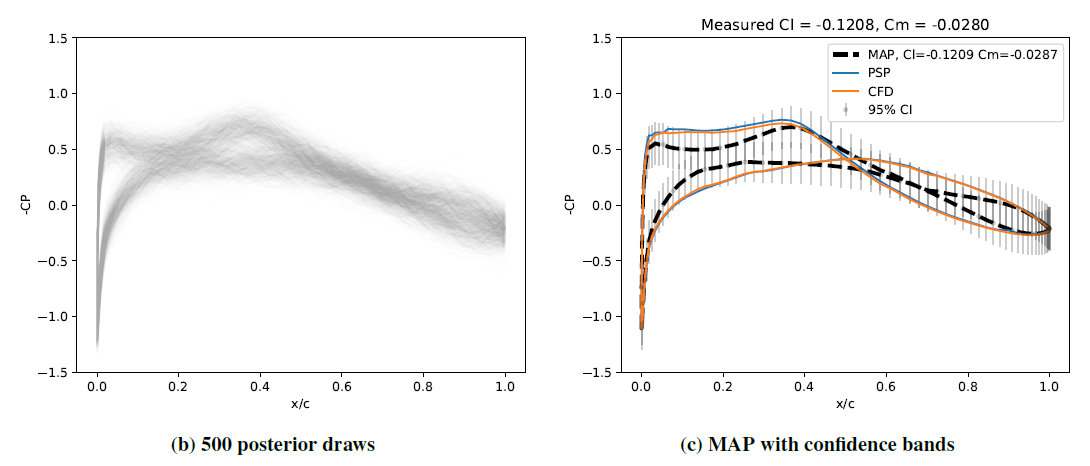
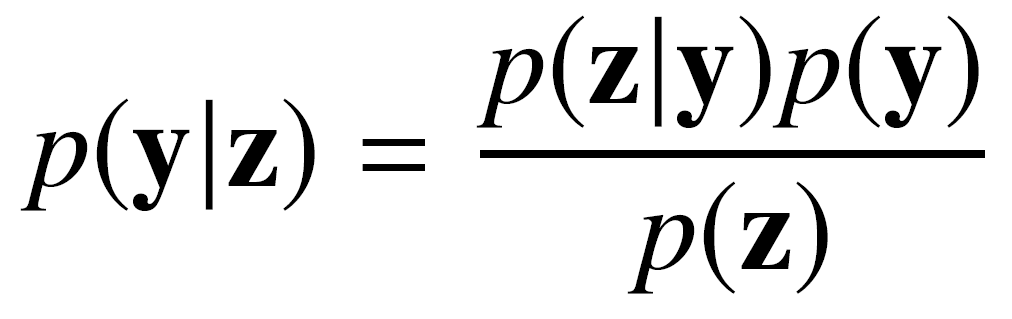
We consider the fusion of two aerodynamic data sets originating from differing fidelity physical or computer experiments. We specifically address the fusion of: 1) noisy and in-complete field from wind tunnel measurements and 2) deterministic but biased fields from numerical simulations. These two data sources are fused in order to estimate the true field that best matches measured quantities of interest that are a function of the field itself. For example, two sources of wing pressure fields are fused based on measured forces and moments on the entire aircraft. We employ a Bayesian framework to infer the true fields conditioned on measured values of the quantities of interest. Essentially we perform a statistical correction to the fields obtained from physical and computer experiments. Additionally, we also show how to propagate the uncertainty in the original data into the fused data.
We are interested solving the linear inverse problem of inferring the unknown field 'y' conditioned on the observations 'z' which include wind-tunnel measurement of integrated quantities such as forces and moments. y and z are related via a linear forward model and the misfit between the model and the noisy observations is quantified by the likelihood z|y. Their relationship between the unknown y, the likelihood model and our prior belief on y is established via the Bayes' rule stated below.
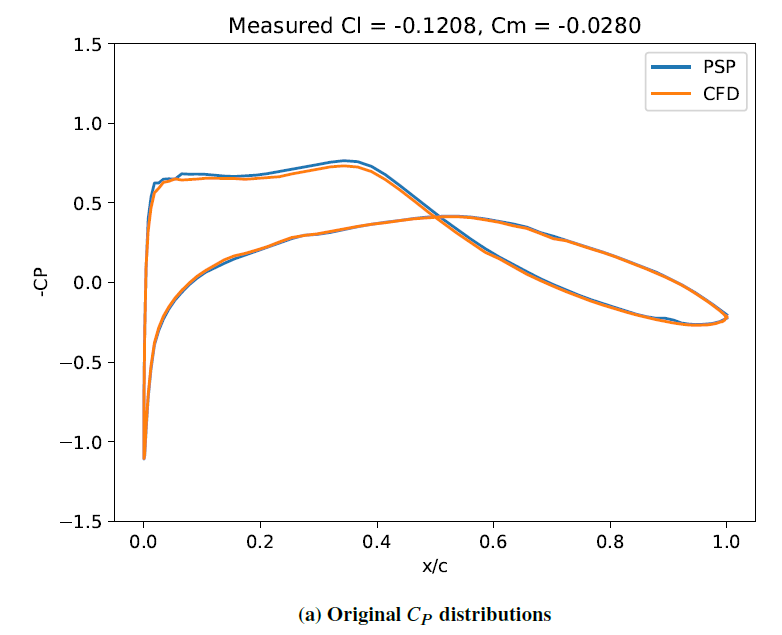
In the figures above, the numerical predictions of the CP (coefficient of pressure) distributions about a wing-section and their wind-tunnel measurements of CP (labeled 'PSP') are shown in (a). While they appear to match each other, the observations 'z' (lift force and pitching moment) does not agree perfectly with our forward model. Therefore Bayesian inference is used to adjust the CP distributions such that they match the measurements. The specified noise levels in 'z' determines how much adjustment is made to the CP curves.
Publications
-
Renganathan, S. A., Harada, K., & Mavris, D. N. (2020). "Aerodynamic Data Fusion Toward the Digital Twin Paradigm." AIAA Journal, 1-17. https://doi.org/10.2514/1.J059203
-
Renganathan, S.A. et al, (2019) "Multi-fidelity data fusion via Bayesian inference", AIAA Aviation Forum
-
Renganathan, S.A., Harada, K, and Mavris, D.N., (2019+) "Aerodynamic Data Fusion Towards the Digital Twin Paradigm", arXiv. under review.
MODEL CALIBRATION & UNCERTAINTY QUANTIFICATION
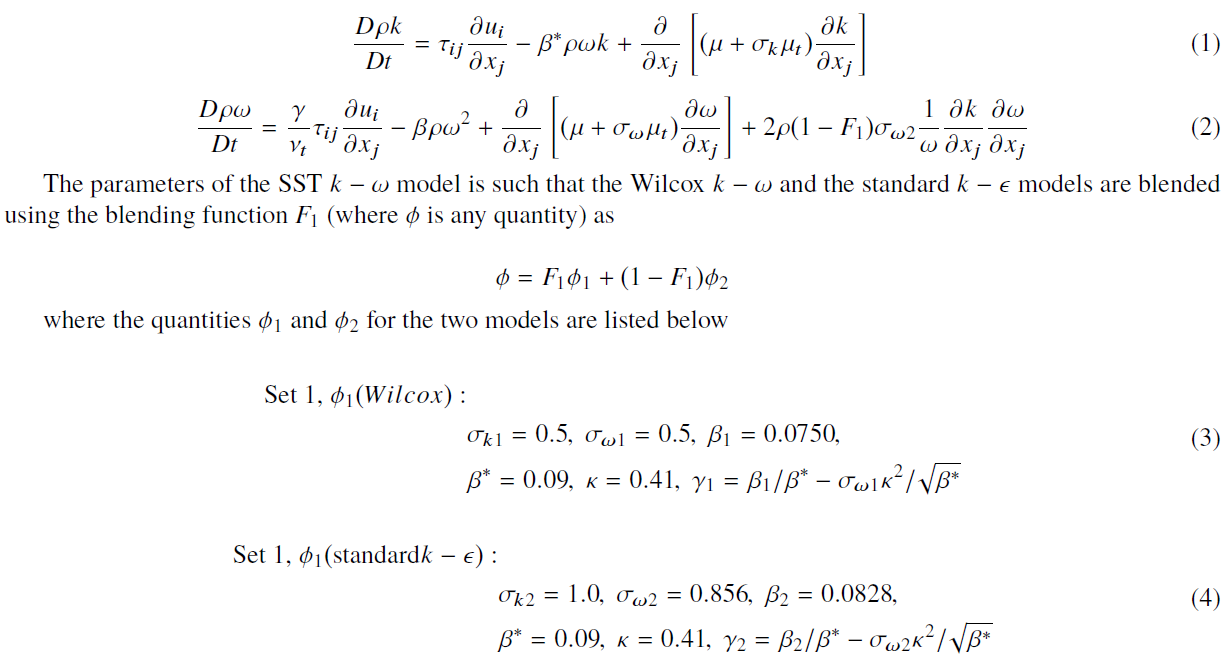
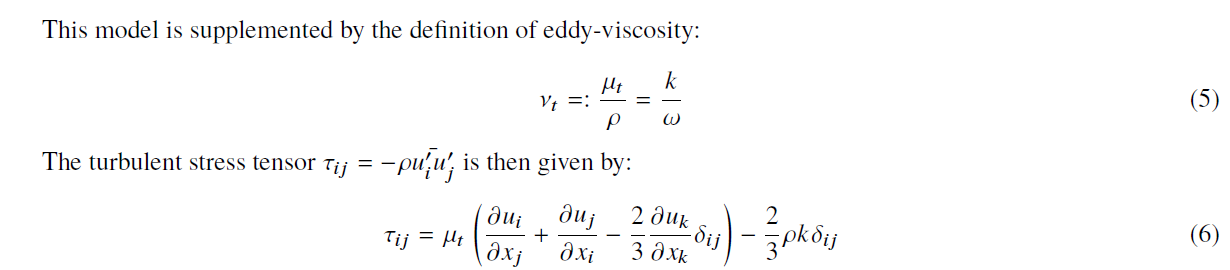
In the design of complex engineering systems such as aircraft and rotorcraft, Reynolds Averaged Navier Stokes (RANS) solvers provide a good trade-off between accuracy and computational cost. A fundamental drawback in the RANS model is that the small-scale turbulent phenomena are not grid-resolved and instead modeled with simplifying assumptions. These models inevitably come with tuning/calibration parameters which have no universal value, but need to be customized for a given problem. In this work, we first try to calibrate the model by identifying the best value of the parameters under a range of flow conditions. We use a Bayesian framework to answer 4 primary questions: (i) does the SST model suffer from identifiability issues?, (ii) what are the \emph{optimal} estimates of the model parameters for transonic flight under a range of operating conditionsm, (iii) how much uncertainty does the mis-specification of turbulence model parameter have in quantities of interest (QoI) and finally (iv) how much uncertainty in the model predictions is attributed to model inadequacy. Additionally, we also develop a framework to propagate the posterior parameter uncertainties through the model in order to estimate the uncertainties on the QoI's which may be both scalar and vector valued. The SST turbulence model and associated calibration/tuning parameters are given below.
Publications
-
Renganathan, S.A. and Dimitri N. Mavris, (2018+) "Calibration and uncertainty quantification of the SST turbulence model", in progress